Page 89 - C112211

یگتسویپ و یریذپ قتشم مود سرد

2
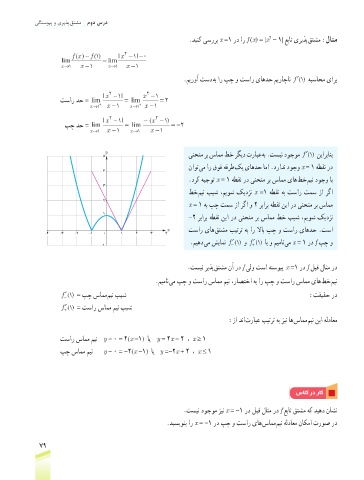
.دینک یسررب x =1 رد ار f (x) = |x - 1| عبات یریذپ قتشم :لاثم
|
f ( ) − f () |x 2 −−10
x
1
lim = lim
x →1 x −1 x →1 x −1
.میروآ تسد هب ار پچ و تسار یاهدح میراچان ()1f ′ هبساحم یارب
|x 2 −1 | x 2 −1
تسار دح = lim = lim = 2
+
+
x →1 x −1 x →1 x −1
2
2
|x −1 | − (x −1 )
پچ دح = lim 2 = lim =−2
() =
x −1
−
x→1 fx x −1 x→1 − x −1
y ′
f
1
5 ینحنم رب سامم طخ رگید ترابع هب .تسین دوجوم () نیاربانب
ناوت یم ار قوف هفرط کی یاهدح اما .درادن دوجو x = 1 هطقن رد
4
.درک هیجوت x = 1 هطقن رد ینحنم رب سامم یاه طخ مین دوجو اب
3
طخ مین بیش ،میوش کیدزن x =1 هطقن هب تسار تمس زا رگا
2
x = 1 هب پچ تمس زا رگا و 2 ربارب هطقن نیا رد ینحنم رب سامم
1
-2 ربارب هطقن نیا رد ینحنم رب سامم طخ بیش ،میوش کیدزن
x تسار یاه قتشم بیترت هب ار لااب پچ و تسار یاهدح .تسا
-4 -3 -2 -1 0 1 2 3 4
1
1
.میهد یم شیامن ′ f () و ′ f () اب و میمان یم x = 1 رد f پچ و
-1 − +
.تسین ریذپ قتشم نآ رد f یلو تسا هتسویپ x =1 رد f لبق لاثم رد

.میمان یم پچ و تسار سامم مین ،راصتخا هب ار پچ و تسار سامم یاه طخ مین

1
− ′ f () = پچ سامم مین بیش :تقیقح رد
′ f + () = تسار سامم مین بیش
1
:زا دنا ترابع بیترت هب زین اه سامم مین نیا هلداعم

تسار سامم مین y - 0 = 2(x -1) ای y = 2x - 2 ، x ≥ 1
پچ سامم مین y - 0 = -2(x -1) ای y =-2x + 2 ، x ≤ 1

سلاک رد راک

.تسین دوجوم زین x = -1 رد لبق لاثم رد f عبات قتشم هک دیهد ناشن

.دیسیونب ار x = -1 رد پچ و تسار یاه سامم مین هلداعم ناکما تروص رد

79