Page 94 - C112211

قتشم 4 لصف

1
f
x
رد قتشم فیرعت زا هدافتسا اب سپس و قتشم عبات زا هدافتسا اب ار f ′)3( .دیروآ تسد هب ار نآ هنماد و قتشم عبات ، )( = رگا :لاثم
x
.دیروآ تسد هب x = 3

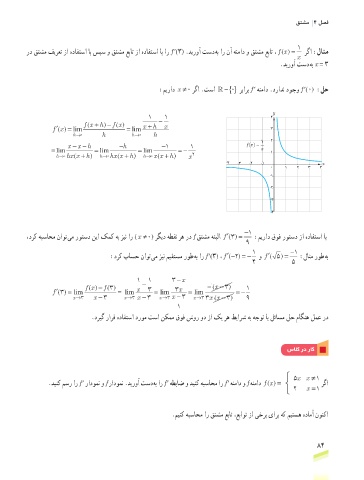
:میراد ≠0x رگا .تسا  − { } 0 ربارب f ′ هنماد .درادن دوجو f ′)0( :لح

y
1 1 4
) +h
f x ( − f )( xh − x
x
+
) ( lim
′ fx = = lim 3
h →0 h h →0 h
1 2
() =
x −−xh −h −1 1 fx
= lim = lim = lim =− x 1
) +h
) +h
) +h
h →0hxx ( h →0hxx ( h →0xx ( x 2
-4 -3 -2 -1 x
0 1 2 3 4
-1
-2
-3
-4
−1
x
،درک هبساحم ناوت یم روتسد نیا کمک هب زین ار ) ≠0( رگید هطقن ره رد f قتشم هتبلا )( =3 :میراد قوف روتسد زا هدافتسا اب
′ f
9
1 −1
:درک باسح ناوت یم زین میقتسم روط هب ار f ′)3( ، ) ′ −2f ( =− و ) ′ 5f ( = :لاثم روط هب
4 5
1 1 3 −x
3
x
f )( − f ) ( x − 3 3x − ) − 3x ( 1
) ( =
f ′ 3 lim = lim = lim = lim =−
) − 3
x →3 x − 3 x →3 x − 3 x →3 x − 3 x →3 3xx ( 9
1
.دریگ رارق هدافتسا دروم تسا نکمم قوف شور ود زا کی ره طیارش هب هجوت اب لئاسم لح ماگنه لمع رد

سلاک رد راک

5 xx ≠1
.دینک مسر ار f ′ رادومن و f رادومن .دیروآ تسد هب ار f ′ هطباض و دینک هبساحم ار f ′ هنماد و f هنماد )(f x = رگا
2 x =1

.مینک هبساحم ار قتشم عبات ،عباوت زا یخرب یارب هک میتسه هدامآ نونکا

84