Page 16 - C112244

تسار طخ رب تکرح :1 لصف

2ـ1 لاثم
و x =-28cm یاه ناکم زا بیترت هب t =74s و t =0s یاه هظحل رد ،تسا تکرح رد x روحم تهج رد هک یکزود شفک
1
2
1
.درذگ یم x =54cm
2
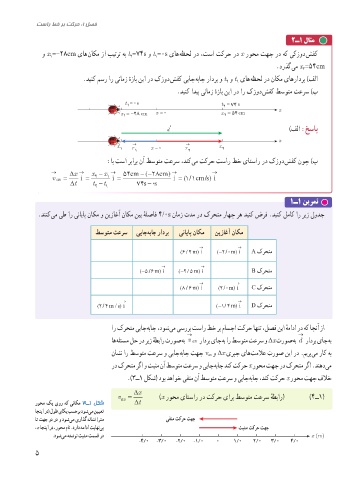
.دینک مسر ار ینامز هزاب نیا رد کزود شفک ییاج هباج رادرب و t و t یاه هظحل رد ناکم یاهرادرب )فلا
ٔ
1
2
t =0s t = 74 s
1
2
x
.دینک ادیپ ینامز هزاب نیا رد ار کزود شفک طسوتم تعرس )ب
x = −28 cm x =0 ٔ x = 54 cm
2
1
t =0s t = 74 s
1
2
x = −28 cm x =0 x = 54 cm x
2
1
→
d )فلا :خساپ
x
x → → → x
1 r x =0 d r 2
1 2
x
:اب تسا ربارب نآ طسوتم تعرس ،دنک یم تکرح تسار طخ یاتسار رد کزود شفک نوچ )ب
x 1 r → x =0 r → x 2
1
→ ∆x → x −x → 54cm −−28cm ) → 2 →
(
( /
v av = i = 2 1 i = i = 11cm /) i
s
∆ t 2 −t t 1 74ss
−
0
1ـ1 نیرمت
.دننک یم یط ار ینایاپ ناکم و نیزاغآ ناکم نیب هلصاف 4/0s نامز تدم رد کرحتم راهچ ره دینک ضرف .دینک لماک ار ریز لودج
ٔ
طسوتم تعرس ییاج هباج رادرب ینایاپ ناکم نیزاغآ ناکم
→ →
)
)
(/ 64m i ( − / 20m i A کرحتم
→ →
( − / 56m i ( − / 25m i B کرحتم
)
)
→ →
)
)
20
(/ 86m i (/ m i C کرحتم
→ →
)
)
(/ 24m /s i ( − / 14m i D کرحتم
ار کرحتم ییاج هباج ،دوش یم یسررب تسار طخ رب ماسجا تکرح اهنت ،لصف نیا همادا رد هک اجنآ زا
ٔ
→ →
اه هلئسم لح رد ریز هطبار تروص هب v رادرب یاج هب ار طسوتم تعرس و Δx تروص هب d رادرب یاج هب
av
ٔ
ناشن ار طسوتم تعرس و ییاج هباج تهج v av و Δx یربج یاه تملاع تروص نیا رد .میرب یم راک هب
رد کرحتم رگا و تبثم نآ طسوتم تعرس و ییاج هباج دنک تکرح x روحم تهج رد کرحتم رگا .دنهد یم
.)3ــ1 لکش( دوب دهاوخ یفنم نآ طسوتم تعرس و ییاج هباج ،دنک تکرح x روحم تهج فلاخ
∆ x
v av = )x روحم یاتسار رد تکرح یارب طسوتم تعرس هطبار( )4ــ1(
ٔ
روحم کی یور هک یناکم 3ــ1 لکش t ∆
اجنیا رد( لوط یاکی بسحرب دوش یم نییعت
ات تهج ود رد و دوش یم یراذگ هناشن )رتم یفنم تکرح تهج
،x اجنیا رد ،روحم مان .دراد همادا تیاهن یب تبثم تکرح تهج
.دوش یم هتشون تبثم تمسق رد x (m)
-4/0 -3/0 -2/0 -1/0 0 1/0 2/0 3/0 4/0
5