Page 21 - C112244

3 کیزیف

x 7 ـ1 لاثم
d 2
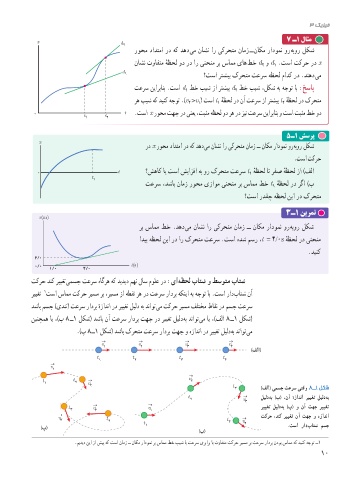
روحم دادتما رد هک دهد یم ناشن ار یکرحتم نامز ــ ناکم رادومن ور هبور لکش
ناشن توافتم هظحل ود رد ار ینحنم رب سامم یاه طخ d و d .تسا تکرح رد x
ٔ
1
2
؟تسا رتشیب کرحتم تعرس هظحل مادک رد .دنهد یم
d 1
تعرس نیاربانب .تسا d طخ بیش زا رتشیب d طخ بیش ،لکش هب هجوت اب :خساپ
2
1
ره بیش هک دینک هجوت .)v <v ( تسا t هظحل رد نآ تعرس زا رتشیب t هظحل رد کرحتم
1 ٔ
2 ٔ
2
1
0 t .تسا x روحم تهج رد ینعی ،تبثم هظحل ود ره رد زین تعرس نیاربانب و تسا تبثم طخ ود
t 1 t 2
5ـ1 شسرپ
x
رد x روحم دادتما رد هک دهد یم ناشن ار یکرحتم نامز ــ ناکم رادومن ور هبور لکش
.تسا تکرح

1 ٔ
ٔ
0 t ؟شهاک ای تسا شیازفا هب ور کرحتم تعرس t هظحل ات رفص هظحل زا )فلا
t 1
تعرس ،دشاب نامز روحم یزاوم ینحنم رب سامم طخ t هظحل رد رگا )ب
1 ٔ
؟تسا ردقچ هظحل نیا رد کرحتم
3ـ1 نیرمت
m
x ()
رب سامم طخ .دهد یم ناشن ار یکرحتم نامز ــ ناکم رادومن ور هبور لکش
ادیپ هظحل نیا رد ار کرحتم تعرس .تسا هدش مسر ،t = 4/0s هظحل رد ینحنم
ٔ
.دینک
6/0
0/0 1/0 4/0 t () s

تکرح دنک رییغت یمسج تعرس هاگره هک دیدید مهن لاس مولع رد :یا هظحل باتش و طسوتم باتش

1
رییغت تسا سامم تکرح ریسم رب ،ریسم زا هطقن ره رد تعرس رادرب هکنیا هب هجوت اب .تسا راد باتش نآ
دشاب مسج )یدنت( تعرس رادرب هزادنا رد رییغت لیلد هب دناوت یم تکرح ریسم فلتخم طاقن رد مسج تعرس
ٔ
نینچمه ای ،)ب 8 ــ1 لکش( دشاب نآ تعرس رادرب تهج رد رییغت لیلد هب دناوت یم ای ،)فلا 8 ــ1 لکش(
.)پ 8 ــ1 لکش( دشاب کرحتم تعرس رادرب تهج و هزادنا رد رییغت لیلد هب دناوت یم
→ → → →
v v v v
1 2 3 4
)فلا(
t 1 t 2 t 3 t 4
→
v
1
→
t t → v 2
1 2 v
2 t 3 )فلا( یمسج تعرس یتقو 8 ــ١ لکش
t 2 → 3 لیلد هب )ب( ،نآ هزادنا رییغت لیلد هب
v
ٔ
t v → v → رییغت لیلد هب )پ( و نآ تهج رییغت
3 4 1
→
v t → تکرح ،دنک رییغت نآ تهج و هزادنا
3 4 t v
t 1 4 4
)پ( .تسا راد باتش مسج
)ب(
.میدید نیا زا شیپ هک تسا نامز ــ ناکم رادومن رب سامم طخ بیش اب تعرس یربارب اب توافتم تکرح ریسم رب تعرس رادرب ندوب سامم هک دینک هجوت ــ١
10