Page 24 - C112244

تسار طخ رب تکرح :1 لصف

5ـ1 نیرمت
v (m/s)
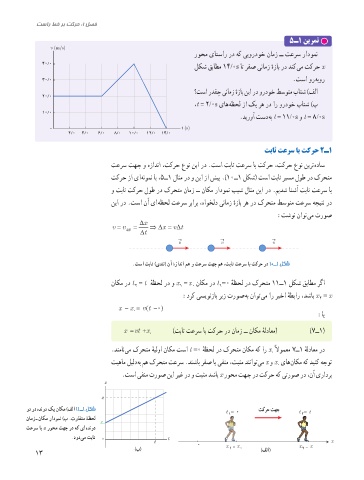
روحم یاتسار رد هک ییوردوخ نامز ــ تعرس رادومن
40/0
لکش قباطم 14/0s ات رفص ینامز هزاب رد دنک یم تکرح x
ٔ
30/0 .تسا ور هبور

؟تسا ردقچ ینامز هزاب نیا رد وردوخ طسوتم باتش )فلا
20/0 ٔ
،t = 2/0s یاه هظحل زا کی ره رد ار وردوخ باتش )ب
10/0
.دیروآ تسد هب t = 11/0s و t = 8 /0s
0 t (s)
2/0 4/0 6/0 8/0 10/0 12/0 14/0

تباث تعرس اب تکرح 2ـ1

تعرس تهج و هزادنا ،تکرح عون نیا رد .تسا تباث تعرس اب تکرح ،تکرح عون نیرت هداس

تکرح زا یا هنومن اب ،5ــ1 لاثم رد و نیا زا شیپ .)10ــ1 لکش( تسا تباث ریسم لوط رد کرحتم
و تباث تکرح لوط رد کرحتم نامز ــ ناکم رادومن بیش لاثم نیا رد .میدش انشآ تباث تعرس اب

نیا رد .تسا نآ یا هظحل تعرس ربارب ،هاوخلد ینامز هزاب ره رد کرحتم طسوتم تعرس هجیتن رد
ٔ
:تشون ناوت یم تروص
∆x
v
x
v = v av = ⇒ ∆ = ∆t
∆t
→ → →
v v v
.تسا تباث )یدنت( نآ هزادنا مه و تعرس تهج مه ،تباث تعرس اب تکرح رد ١0ــ١ لکش
ٔ

ناکم رد t = t هظحل رد و x =x ناکم رد t =0 هظحل رد کرحتم 11ــ1 لکش قباطم رگا
2 ٔ 1 0 1 ٔ
:درک یسیونزاب ریز تروص هب ناوت یم ار ریخا هطبار ،دشاب x = x
ٔ
2
x - x = v )t -0(
0
:ای

x = vt +x )تباث تعرس اب تکرح رد نامز ــ ناکم هلداعم( )7ــ1(
0 ٔ
.دنمان یم کرحتم هیلوا ناکم تسا t =0 هظحل رد کرحتم ناکم هک ار x لاومعم 7ــ1 هلداعم رد
0ً
ٔ
ٔ
ٔ
تیهام لیلد هب مه کرحتم تعرس .دنشاب رفص ای یفنم ،تبثم دنناوت یم x و x یاه ناکم هک دینک هجوت
0
.تسا یفنم تروص نیا ریغ رد و تبثم دشاب x روحم تهج رد تکرح هک یتروص رد ،نآ یرادرب
x
x
ود رد هدنود کی ناکم )فلا ١١ ــ١ لکش تکرح تهج
=
=
t 0 t t
2
1
نامز ـ ناکم رادومن )ب .توافتم ۀظحل
x 0
تعرس اب x روحم تهج رد هک یا هدنود
.دود یم تباث 0 t
t 0 x
=
=
1
2
)ب( x x 0 )فلا( x x
13