Page 66 - C112244

جاوما و ناسون :3 لصف

هداس گنهامه تکرح 2ـ3
ناکم
T یاه ناسون زا رگید هنومن ود ،3ــ3 لکش .میدش انشآ یا هرود ناسون کی زا یا هنومن اب شیپ شخب رد
ٔ
ناسون یلو ،دنتسه یا هرود اه ناسون نیا یود ره .دهد یم ناشن اهنآ نامز ــ ناکم رادومن مسر اب ار یا هرود
0 t
2
1
هتفگ )SHM( هداس گنهامه تکرح ،یسونیس یاه ناسون هب .تسا هداد خر یسونیس روط هب ،ب 3ــ3 لکش
)فلا(
ناکم رتلااب حوطس رد اریز تسا رگید یا هرود ناسون عون ره کرد یارب ییانبم ،هداس گنهامه تکرح .دوش یم
T
.تفرگ رظن رد یسونیس یاه ناسون زا یعومجم ناوت یم ار یا هرود ناسون ره هک دوش یم هداد ناشن
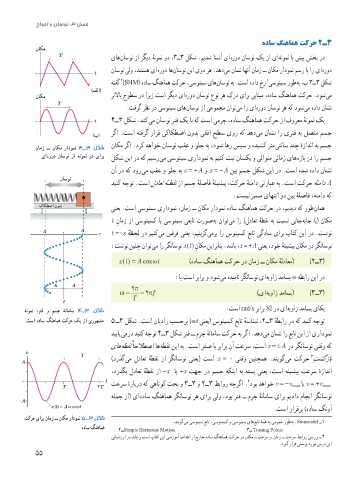
0 t 4ــ3 لکش .دنک یم ناسون رنف کی اب هک تسا یمرج ،هداس گنهامه تکرح زا فورعم هنومن کی
ٔ
رگا .تسا هتفرگ رارق یکاکطصا نودب یقفا حطس یور هک دهد یم ناشن ار یرنف هب لصتم مسج
)ب(
ناکم رگا .درک دهاوخ ناسون بقع و ولج هب ،دوش اهر سپس و هدیشک رتم یتناس دنچ هزادنا هب مسج
نامز ــ ناکم رادومن 3ــ3 لکش ٔ
یا هرود ناسون زا هنومن ود یارب لکش نیا رد هک میسر یم یسونیس یرادومن هب مینک تبث ناسکی و یلاوتم ینامز یاه هزاب رد ار مسج

نآ رد هک دور یم بقع و ولج هب x = +A و x = -A نیب مسج لکش نیا رد .تسا هدش هداد ناشن
ناسون
دینک هجوت .تسا لداعت هـطقن زا مسج هلصاف هنیشیب ،تکرح هنماد یترابع هب .تسا تکرح هنماد A
ٔ
ٔ
ٔ
ٔ
ٔ
.تسین ریسم یاهتنا ود نیب هلصاف ،هنماد هک
ٔ
کاکطصا نودب
ینعی .تسا یسونیس یرادومن ،نامز ــ ناکم رادومن هداس گنهامه تکرح رد ،میدید هک روط نامه
ِ
t نامز زا یسونیسک ای یسونیس یعبات تروص هب ناوت یم ار )لداعت هطقن هب تبسن ییاج هباج ای( ناکم
ٔ
- A 0 A x t = 0 s هظحل رد مینک یم ضرف ینعی ،مینیزگ یمرب ار سونیسک عبات یگداس یارب باتک نیا رد .تشون
ٔ
ِ
:تشون نینچ ناوت یم ار رگناسون x (t ) ناکم نیاربانب .دشاب ،x = +A ینعی ،دوخ هنیشیب ناکم رد رگناسون
ٔ
x (t ) = A cos ω t )هداس گنهامه تکرح رد نامز ــ ناکم هلداعم( )2ــ3(
ٔ
:اب تسا ربارب و دوش یم هدیمان رگناسون یا هیواز دماسب ω هطبار نیا رد
A A 2 π
ω= = 2 f π )یا هیواز دماسب( )3ــ3(
T
t
.تسا rad/s ربارب SI رد یا هیواز دماسب یاکی
ۀنومن ،رنف و مسج ۀناماس 4ــ3 لکش

.تسا هداس گنهامه تکرح کی زا یروهشم 5 ــ3 لکش .تسا نایدار بسحرب )ωt ینعی( سونیسک عبات هسانش ،2ــ3 هطبار رد هک دینک هجوت
ٔ
ٔ
دیبای یمرد دینک هجوت 4ــ3 لکش رنف ــ مرج هناماس تکرح هب رگا .دهد یم ناشن ار عبات نیا زا یرادومن
ٔ
یاه هطقن ًاحلاطصا اه هطقن نیا هب .تسا رفص اب ربارب نآ تعرس ،تسا x = ± A رد رگناسون یتقو هک
x
3 ِ
T )درذگ یم لداعت هطقن زا رگناسون ینعی( تسا x = 0 یتقو نینچمه .دنیوگ یم تکرح تشگزاب
A ٔ

،درذگب لداعت هطقن زا -x ای +x تهج رد مسج هکنیا هب هتسب ینعی ،تسا هنیشیب تعرس هزادنا
ٔ
ٔ
0 t تعرس هرابرد هک یهاتوک ثحب و 3ــ3 و 2ــ3 طباور هچرگا . دوب دهاوخ v = -v max ای v = +v max
4
T 2T ٔ
هلمج زا( یا هداس گنهامه رگناسون ره یارب یلو ،دوب رنف ــ مرج هناماس یارب میداد ماجنا رگناسون
ٔ
-A
x(t) = A cosωt .تسا رارقرب )هداس گنوآ
v x تکرح یارب نامز ــ ناکم رادومن 5 ــ3 لکش
T .دنیوگ یم یسونیس عبات ،یسونیسک و یسونیس یاه عبات همه هب یمومع روط هب .Sinusoidal ــ1
ٔ
v max هداس گنهامه
2ــSimple Harmonic Motion 3ــ Turning Points
یبایشزرا رد دیابن و تسا باتک نیا یشزومآ فادها زا جراخ هداس گنهامه تکرح رد ناکم ــ تعرس و نامز ــ تعرس طباور یسررب ــ4
.دریگ رارق شسرپ دروم سرد نیا
0 t
55 T 2T
- v max
v x (t)= - v max sinωt