Page 69 - C112244

3 کیزیف

هداس گنهامه تکرح رد یژرنا 3ـ3
هناماس نیا .دهد یم ناشن کاکطصا نودب یقفا حطس یور ناسون ماگنه ار یرنف ــ مرج هناماس 6 ــ3 لکش k
ٔ
m v
هناماس رد دوش یم هدیشک ای هدرشف یرنف یتقو دیدید 1 کیزیف باتک رد .تسا هداس گنهامه تکرح زراب لاثم
ٔ
x
رنف هک ییاج( لداعت هطقن زا ییاج هباج شیازفا اب هک یروط هب ،دوش یم هریخذ یناسشک لیسناتپ یژرنا رنف ــ مرج -A 0 x A
ٔ
رنف ــ مرج هناماس لیسناتپ یژرنا نیاربانب .دبای یم شیازفا لیسناتپ یژرنا نیا )تسا هدش هدیشک هن و هدرشف هن
ٔ
.تسا رفص ربارب )x = 0( لداعت هطقن رد و هنیشیب )x = ±A( یتشگزاب طاقن رد یور ناسون رد رنف ــ مرج ۀناماس 6 ــ3 لکش
ٔ
کاکطصا نودب یقفا حطس
1
2
K = mv اب ربارب و دراد یگتسب نآ یدنت و رنف هب لصتم هعطق مرج هب زین هناماس نیا یشبنج یژرنا
ٔ
2
یروط ،دوش یم مک زین هناماس یشبنج یژرنا و دبای یم شهاک یدنت ،لداعت هطقن زا ییاج هباج شیازفا اب .تسا
ٔ
رد یدنت هنیشیب .دسر یم رفص هب هناماس یشبنج یژرنا دوش یم رفص یدنت هک x = ±A یتشگزاب طاقن رد هک
ٔ
.دوش یم هنیشیب هطقن نیا رد زین یشبنج یژرنا نیاربانب و دهد یم خر x = 0 ِ لداعت هطقن
ٔ
یژرنا و یشبنج یژرنا عومجم اب ربارب هناماس نیا یکیناکم یژرنا هک میتخومآ 1 کیزیف رد
هتسیاپ هناماس یکیناکم یژرنا ،تسا کاکطصا نودب حطس نوچ .(E =K+U ) تسا نآ لیسناتپ
هطقن ره و ،لداعت هطقن ،یتشگزاب طاقن رد لیسناتپ و یشبنج یاه یژرنا عومجم نیاربانب و دنام یم
ٔ
ٔ
،لداعت هطقن زا ییاج هباج شیازفا اب هک هزادنا نامه هب .تسا ربارب مه اب ریسم زا یرگید هاوخلد
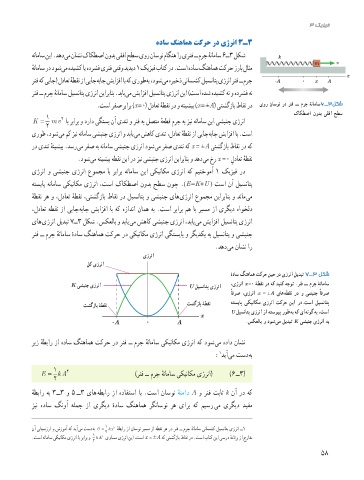
یاه یژرنا لیدبت 7ــ3 لکش .سکعلاب و دبای یم شهاک یشبنج یژرنا ،دبای یم شیازفا لیسناتپ یژرنا

رنف ــ مرج هناماس هداس گنهامه تکرح رد یکیناکم یژرنا یگتسیاپ و رگیدکی هب لیسناتپ و یشبنج
ٔ
ٔ
.دهد یم ناشن ار
یژرنا
لک یژرنا
ۀداس گنهامه تکرح نیح رد یژرنا لیدبت 7ــ3 لکش
K یشبنج یژرنا U لیسناتپ یژرنا ،یژرنا x =0 ۀطقن رد هک دینک هجوت .رنف ــ مرج ۀناماس
ًافرص ،یژرنا x = ±A یاه هطقن رد و یشبنج ًافرص
تشگزاب ۀطقن تشگزاب ۀطقن هتسیاپ یکیناکم یژرنا تکرح نیا رد.تسا لیسناتپ
U لیسناتپ یژرنا زا هتسویپ روط هب هک یا هنوگ هب ،تسا
x
-A 0 A .سکعلاب و دوش یم لیدبت K یشبنج یژرنا هب

ریز هطبار زا هداس گنهامه تکرح رد رنف ــ مرج هناماس یکیناکم یژرنا هک دوش یم هداد ناشن
ٔ
ٔ
1
: دیآ یم تسد هب
1
E = kA 2 )رنف ــ مرج هناماس یکیناکم یژرنا( )6 ــ3(
ٔ
2
هطبار هب 3ــ3 و 5 ــ3 یاه هطبار زا هدافتسا اب .تسا ناسون هنماد A و رنف تباث k نآ رد هک
ٔ
ٔ
زین هداس گنوآ هلمج زا یرگید هداس گنهامه رگناسون ره یارب هک میسر یم یرگید دیفم
ٔ
1
2
نآ یبایشزرا و شزومآ هک دیآ یم تسد هب U = 2 kx هطبار زا ناسون ریسم زا هطقن ره رد رنف ــ مرج هناماس یناسشک لیسناتپ یژرنا ــ1
ٔ
ٔ
1
.تسا هناماس یکیناکم یژرنا اب ربارب و kA یواسم یژرنا نیا ،تسا x = ±A هک یتشگزاب طاقن رد .تسا باتک نیا یسرد همانرب زا جراخ
2
ٔ
2
58